It’s a poor sort of memory that only works backward.—- Lewis Carroll
1 背景
时钟(Clock):其精确的硬件实现通常基于振荡器,其在两个信号值0-1,或称“高-低电平”。两个相邻的信号上升沿称为时钟周期,时钟周期非常重要,所有的时序逻辑都是基于时钟周期的,比如写入内存(读取内存是个时序无关操作),内存值的真实修改(假设当前时钟周期进行写入内存操作)是发生在下一个时钟周期上升沿的时候,可以参见书本的多路转换DFF实现。
触发器(Filp-Flops):此项目采用DFF(Data Filp-Flops),DFF有个时钟输入,根据主时钟信号连续地交变。数据和时钟的输入使得DFF能够实现基于时间行为out(t)=in(t-1)
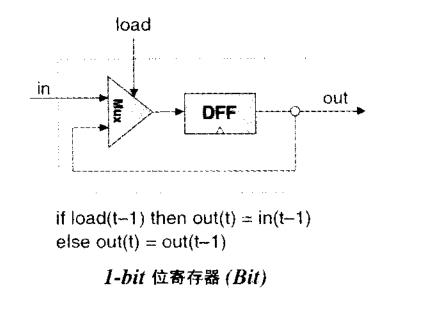
寄存器(register):这里的寄存器指的是广义上的存储设备,并不仅仅是通常意义上的CPU内的register,它的存储行为是out(t)=out(t-1),也就是说他能够输出他上一个时钟周期的输入,并通过Mux(多路转换器)在条件允许(load控制)时输出至输入信号,这也就说明了它为什么能够维持自身的“状态”
2 Memories
作为一个程序员,和内存打交道的时候还是很多的,所以让我们来重点看看内存这个家伙的构造。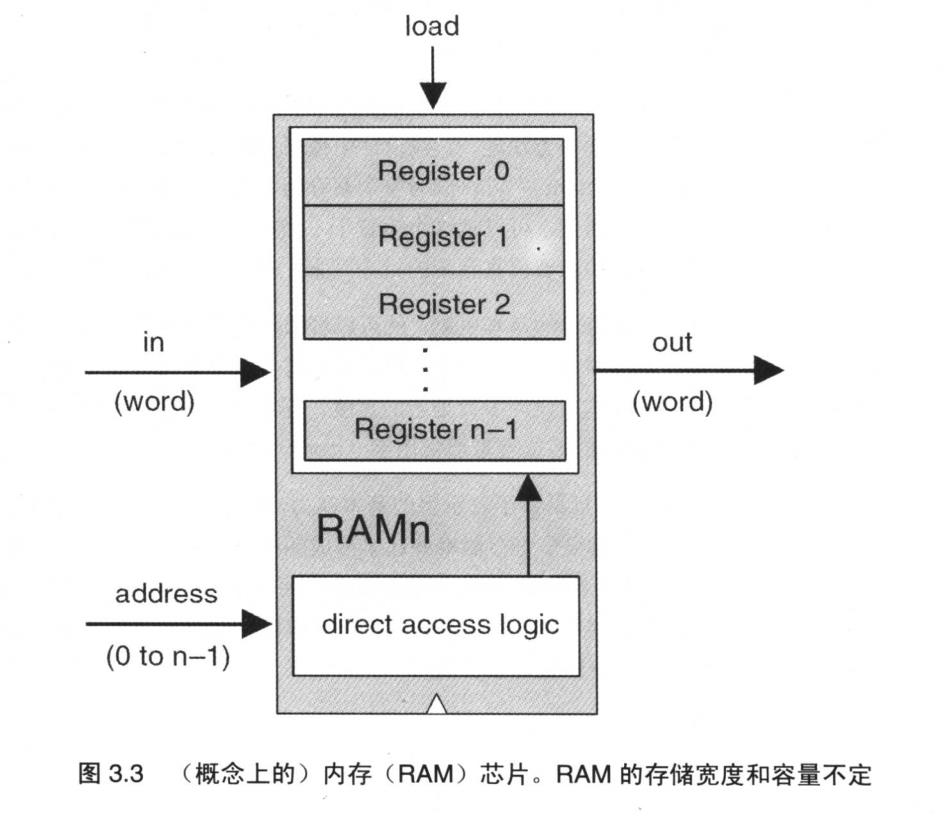
如图3.3所示,内存可以通过将很多寄存器堆叠起来形成随机存取RAM单元来实现。随机存取内存(RAM)这个概念由此得来:在RAM上能够随机访问被选择的字而不会受限于访问顺序。也就是说,我们要求内存中的任何字(无论具体物理位置在哪里)都能以相等的速度被直接访问。
说到这里在数据结构课上老师说的,同学们,我们的数组具有随机性啊,随机性,当时还不太清楚这个随机性到底是怎么实现的,那么现在就真相大白了,数组的随机性实际上就是指RAM的随机性(数组可以理解成在内存中连续的片断,连续很重要,实际上在编译器层面对数组的处理也是看成一段连续的内存)
那么现在让我们一起看看RAM的随机性是如何实现的;-)
注意图3.3的输入管脚有一个address,那么实际上内存是由8个16位寄存器构成的(假定),那么在address处输入的就是3位的电信号,聪明的大家已经想到了,通过3位的电信号经过DMux(多路选择器)选择出一个唯一的8位寄存器位置,比如输入010,那么第一个0代表选择了前二分之一个内存区域(以寄存器数量为单位),010->前四个中的后两个中的第一个,完美的命中了第三个寄存器位置,你看这就完成了内存寻址。。是不是没有你想的那么复杂,当然真实环境下的内存肯定比这里来的复杂,但是这里探索的是模型和原理,具体的细节欢迎大家在评论下面补充说明。
3 时序芯片和逻辑芯片的比较
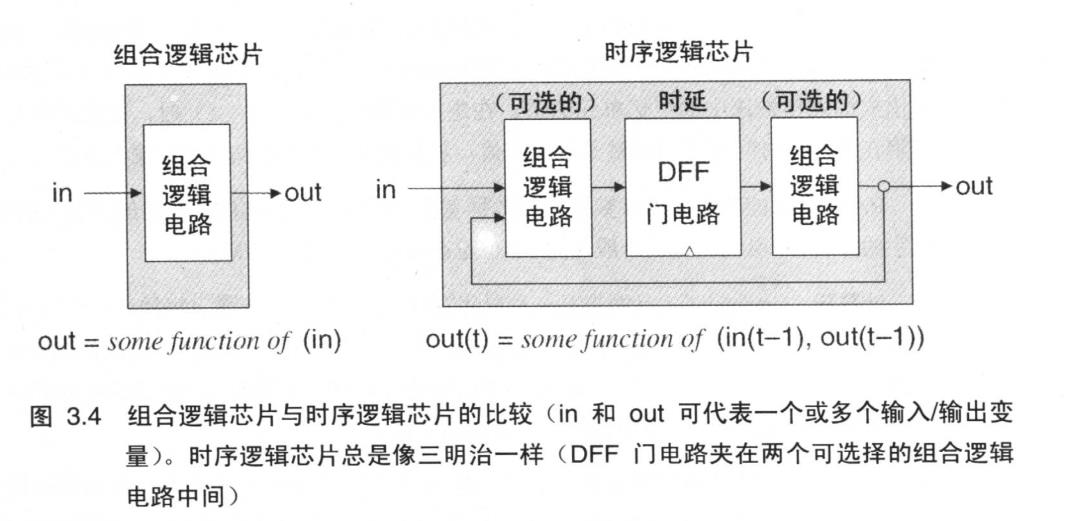
前面说到的组合逻辑芯片的输出随其输入的变化而变化,而不去考虑时间。相比之下,时序结构中包含的DFF保证了它们的输出变化仅仅发生在一个时钟周期到下一个时钟周期的转换点上(比如上升沿),而不在时钟周期内。实际上,我们允许时序芯片在时钟周期之内出现不稳定的状态,但是必须保证在下一个时钟周期的起始点,其输出值是正确的
时序芯片输出这种“离散化(discretization)”过程有个重要作用:它能被用来对整个计算机系统进行同步。
假设指示ALU计算x+y,x和y分别属于距离ALU远近程度不一的RAM(远近程度说明了他们有效的电信号到达ALU的时间),那么由于他俩在不同时刻到达ALU而ALU作为一个组合逻辑毫无时序的概念,它只会不停的从输入管脚读取数据,那么在ALU的两端输入达到稳定前,它只会不断的产生垃圾值。那么如何解决这个问题呢?既然ALU会在某个时间点给出正确的输出并且达到稳定(持续的正确输出..个人理解),在此前是输出垃圾值,那么就可以将ALU的输出连接至一个时序逻辑设备,这个设备在时钟上升沿的时候读取来自ALU的输入,那么如何保证此时读取的输入是正确的呢?这就涉及到了计算机时钟的设定,规定计算机时钟周期的长度要比1个比特在计算机系统中两个物理距离最长的芯片之间传输的时间稍长。这样就
能在时间上保证时序芯片得到了有效的输入值(在下个时钟周期的上升沿)。
通过时序芯片 ,可以将一个个独立的硬件同步为一个协调统一的系统。(第五章小结会有后续说明)
4 本章架构图